Rational function approximation in Julia
Documentation for RationalFunctionApproximation.jl.
This package computes rational approximations of a function or data given in the complex plane. For background reading, see [1], [2] (or the related arXiv version [3]), [4], and [5].
A rational function is a ratio of two polynomials. Rational functions are capable of very high accuracy and, unlike polynomial interpolation, do not require the interpolation nodes to be distributed in a highly restricted way. They are a good choice for approximating functions with singularities or other complicated behavior. Also unlike polynomials, however, they do not depend linearly on the data, which has historically made them difficult to compute and work with.
Here's a smooth, gentle function on the interval
using RationalFunctionApproximation, CairoMakie
CairoMakie.update_theme!(size = (600, 400), fontsize=11)
const shg = current_figure
f = x -> exp(cos(4x) - sin(3x))
lines(-1..1, f)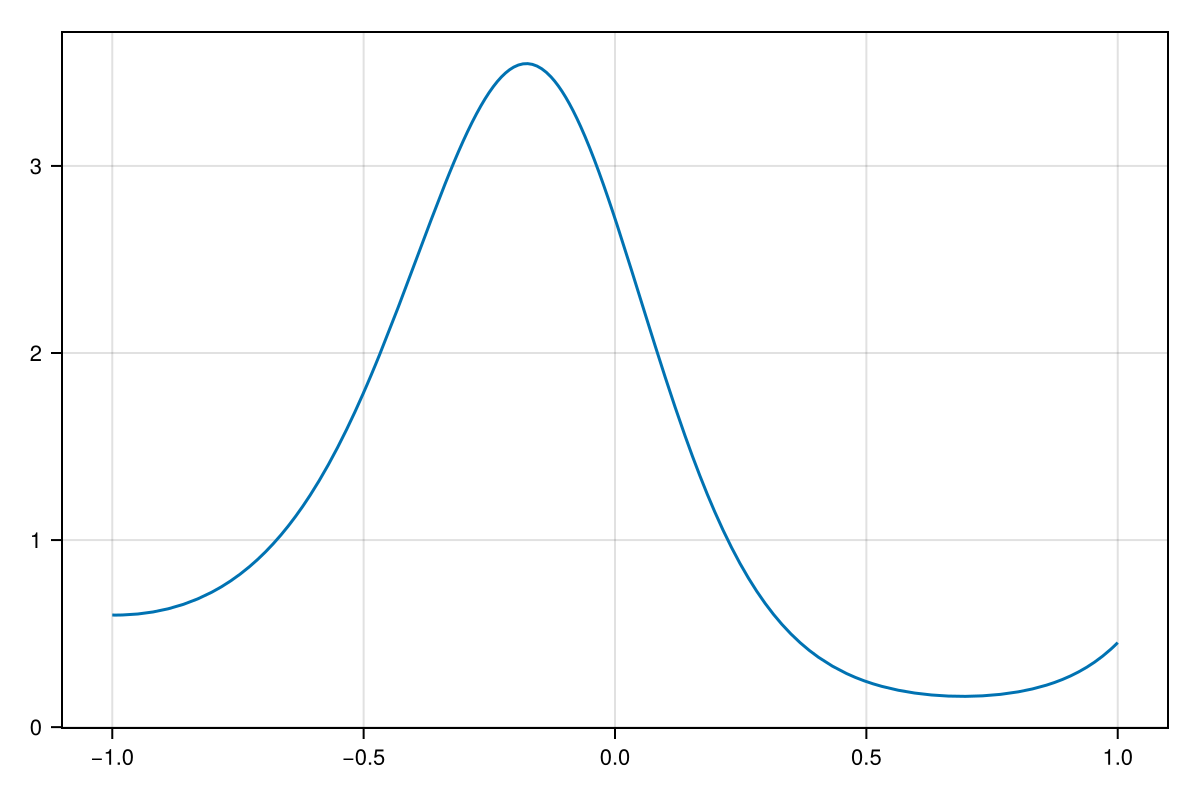
To create a rational function that approximates approximate function:
r = approximate(f, unit_interval)Barycentric{Float64, Float64} rational of type (19, 19) constructed on: Segment(-1.0,1.0)The value of unit_interval is defined by the package to be the interval r is a type (19,19) rational approximant that can be evaluated like a function:
f(0.5) - r(0.5)-6.38378239159465e-16We see that this approximation is accurate to about 13 places over the interval:
z, err = check(r)
lines(z, err)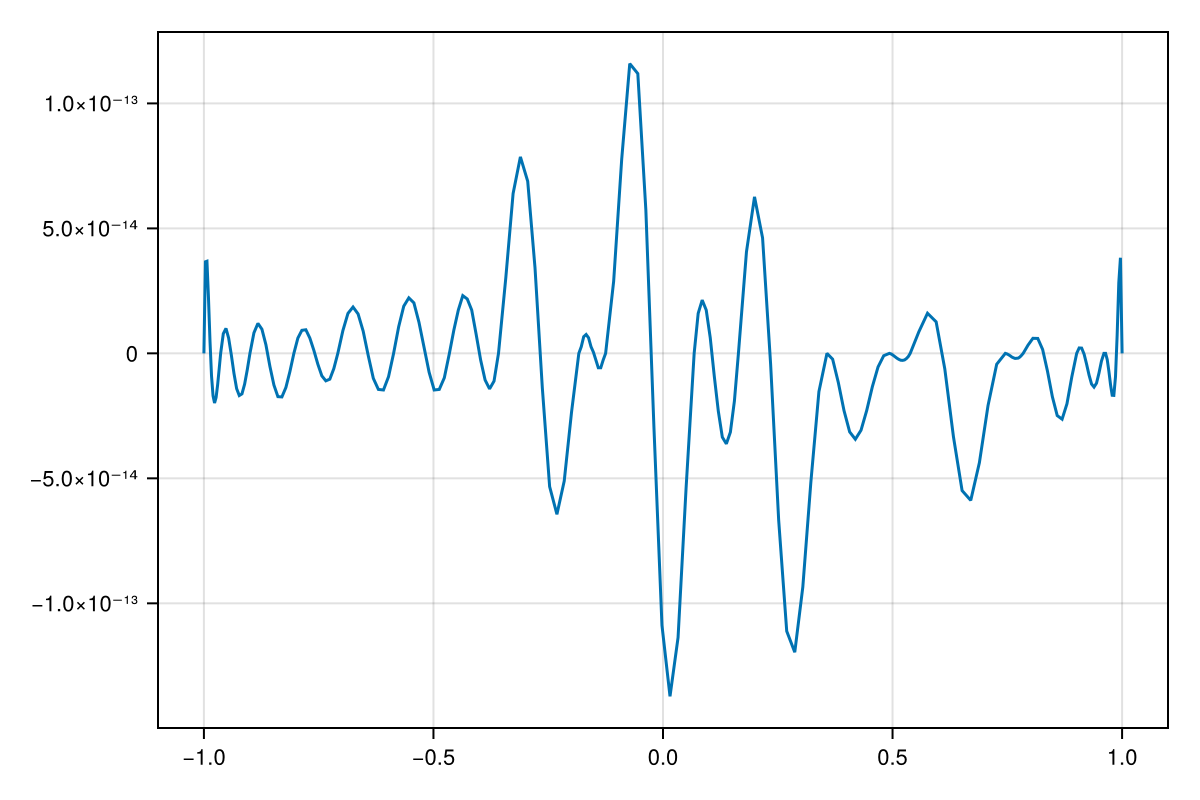
The rational approximant interpolates
x = nodes(r)
scatter!(x, 0*x, markersize = 8, color=:black)
shg()
We could choose to approximate over a wider interval:
using ComplexRegions
r = approximate(f, Segment(-2, 4))Barycentric{Float64, Float64} rational of type (50, 50) constructed on: Segment(-2.0,4.0)Note that the degree of the rational function increased to capture the additional complexity.
One interesting feature of a rational function is that it can have poles, or infinite value, at the roots of the denominator polynomial. In this case, the poles hint at where the function is most sharply peaked:
poleplot(r)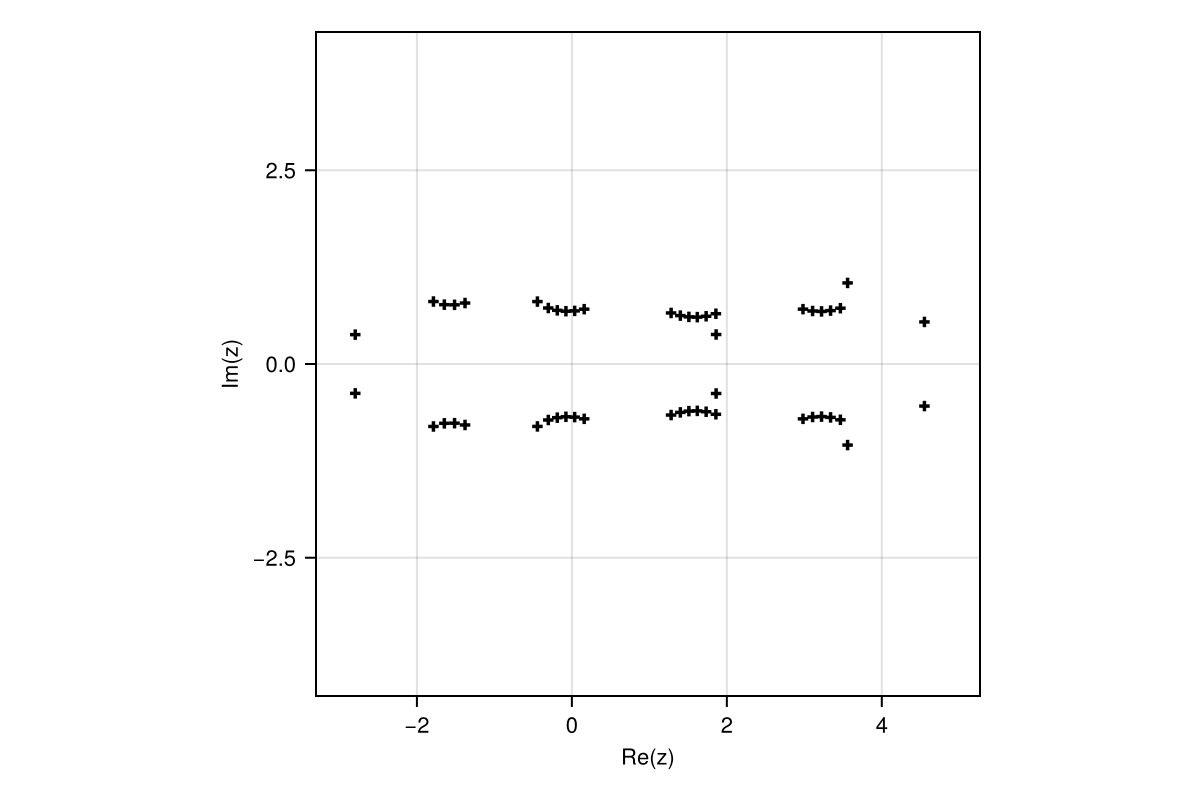
More typically, however, a function that is well-behaved on the real axis has a singularity structure lurking in the complex plane, and the poles of rational functions provide a unique way to cope with them. For instance, let's try approximating the hyperbolic secant function:
r = approximate(sech, Segment(-4, 4))Barycentric{Float64, Float64} rational of type (10, 10) constructed on: Segment(-4.0,4.0)The sech function is smooth on the real axis but has poles on the imaginary axis at odd multiples of
2 * poles(r) / π10-element Vector{ComplexF64}:
-0.8695151907800662 - 6.944383914339748im
-0.8695151907800662 + 6.944383914339748im
-9.779832330514768e-5 - 4.992824452379868im
-9.779832330514767e-5 + 4.9928244523798675im
1.2177609574108157e-13 - 0.9999999999980325im
1.2177609574108157e-13 + 0.9999999999980325im
7.515486115346372e-8 + 3.0000019449351703im
7.515486115346372e-8 - 3.0000019449351703im
0.866695604260018 - 6.940478718053261im
0.866695604260018 + 6.940478718053262imWe can use the DomainColoring package to visualize the rational function in the complex plane. Color is used to show the phase angle of the value, while dark-to-bright cycles of lightness show powers of e in the magnitude. The poles stand out as locations of rapid change in both phase and magnitude.
using DomainColoring
domaincolor(r, 6; abs=true)
lines!(r.domain, linewidth=3, color=:white)
shg()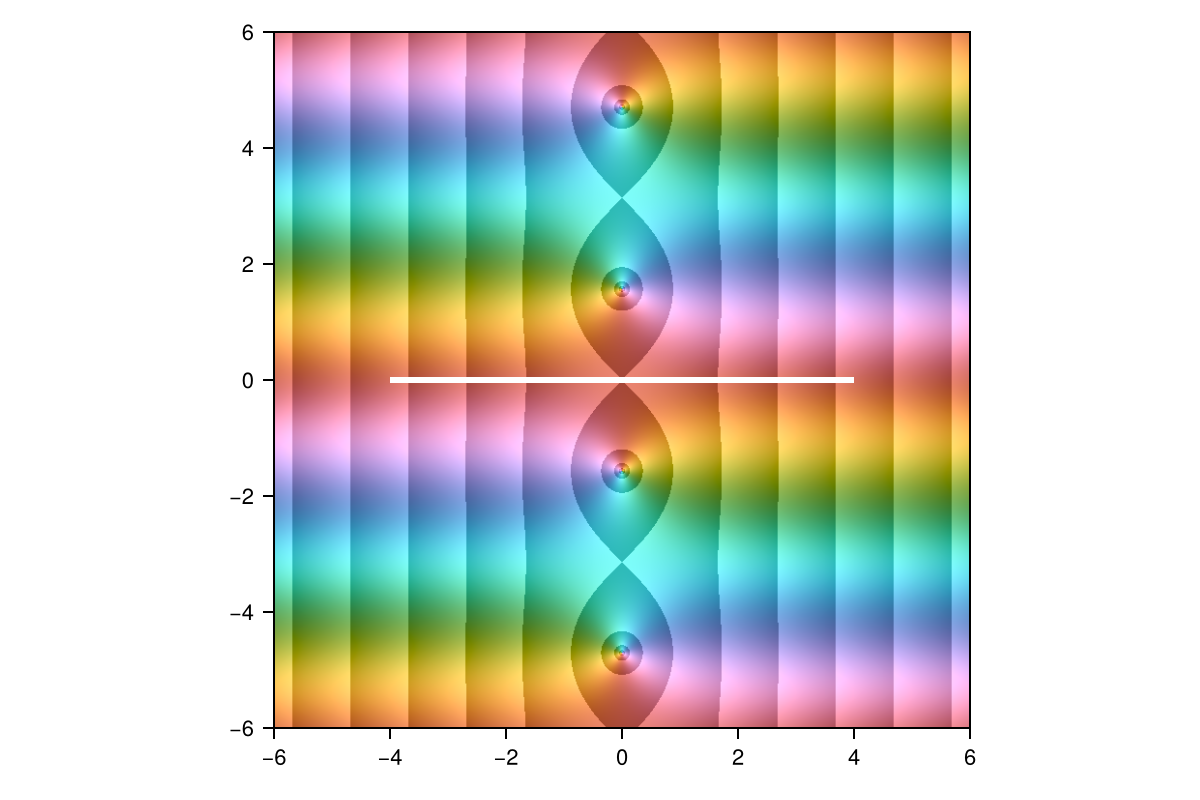
A meromorphic function such as sech has only those isolated poles as singularities, and getting those right is most of the battle. By contrast, the function
f = x -> log(x + 0.05im)
r = approximate(f, unit_interval)
domaincolor(r, 1.2; abs=true)
lines!(r.domain, linewidth=3, color=:white)
shg()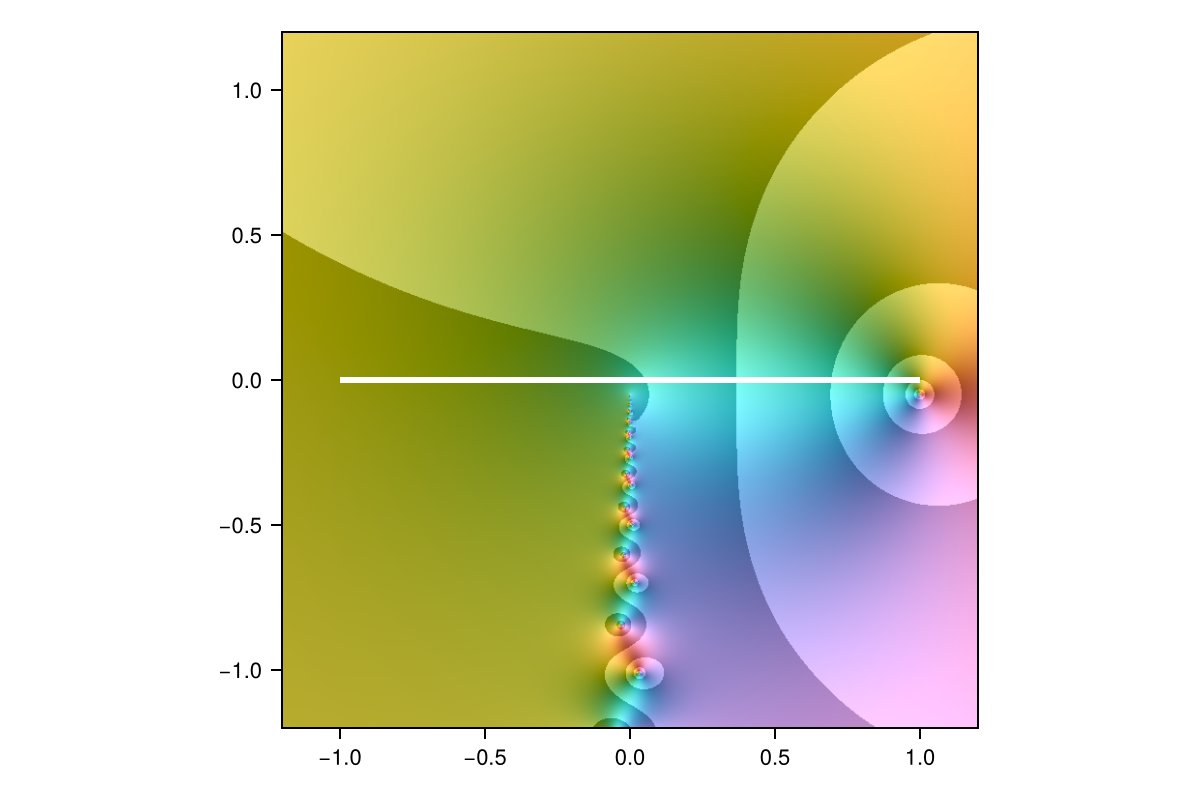
We close this quick introduction with approximation of
r = approximate(abs, unit_interval; tol=1e-12)
convergenceplot(r)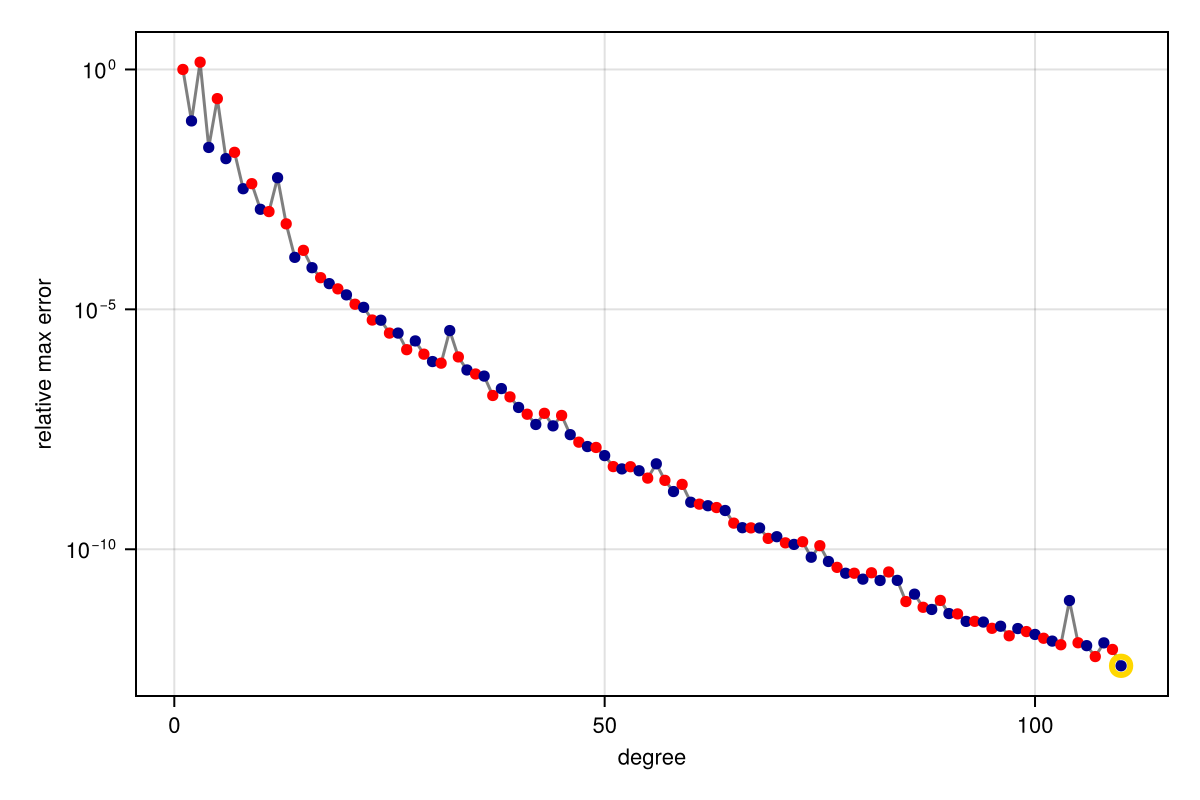
We find that the nodes of the approximant are also distributed (nearly) root-exponentially around the singularity:
z = filter(>(0), nodes(r))
scatter(sort(abs.(z)), axis=(ylabel="| node |", yscale=log10,))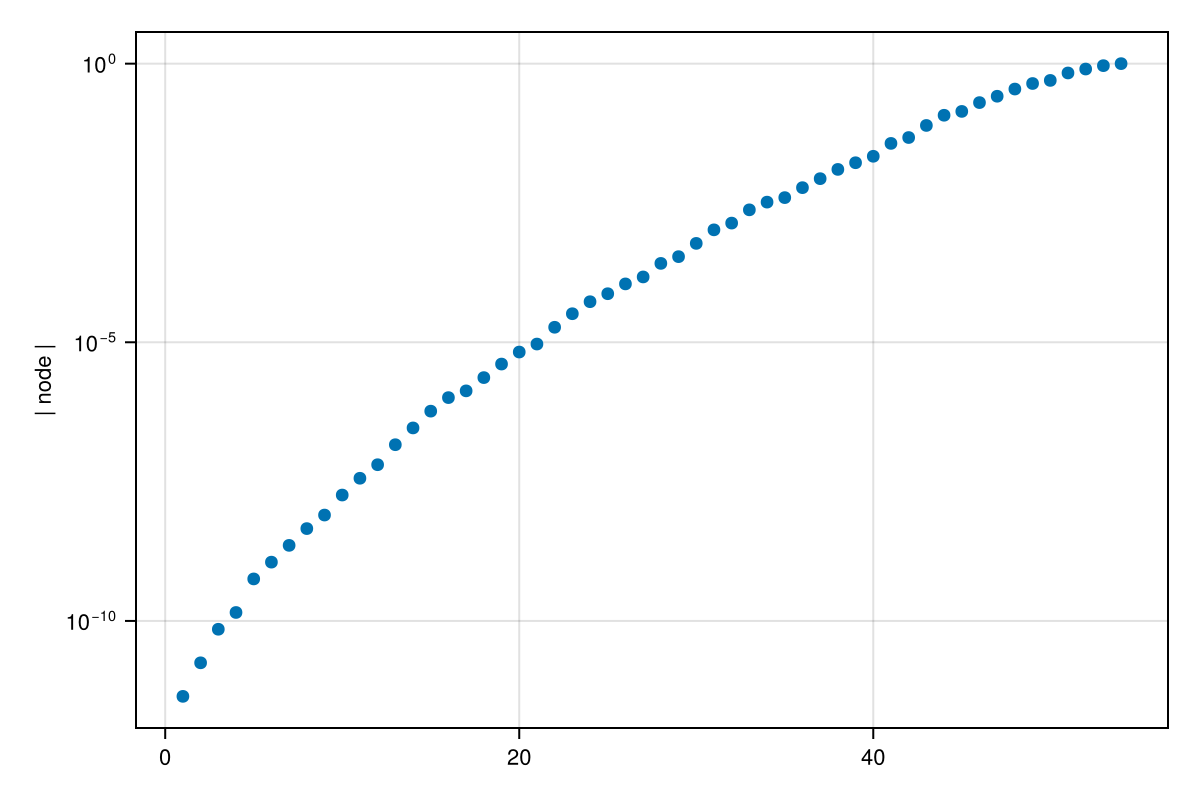
Contents
Algorithms describes the algorithms available for rational approximation.
Approximation on domains shows how to approximate functions on different domains.
Discrete data shows how to approximate data given as points and values rather than as functions.
Minimax approximation explains the difference between the default approximation and minimax approximation.
Usage from Python shows how to use the package from Python.
Functions and types collects the documentation strings of the major package features.
References
Y. Nakatsukasa, O. Sète and L. N. Trefethen. The AAA Algorithm for Rational Approximation. SIAM Journal on Scientific Computing 40, A1494-A1522 (2018). Accessed on Jul 14, 2020.
T. A. Driscoll, Y. Nakatsukasa and L. N. Trefethen. AAA Rational Approximation on a Continuum. SIAM Journal on Scientific Computing 46, A929-A952 (2024). Accessed on May 15, 2025.
T. Driscoll, Y. Nakatsukasa and L. N. Trefethen. AAA Rational Approximation on a Continuum (2023). Accessed on Feb 26, 2024.
S. Costa and L. N. Trefethen. AAA-least Squares Rational Approximation and Solution of Laplace Problems. In: European Congress of Mathematics, 1 Edition, edited by A. Hujdurović, K. Kutnar, D. Marušič, Š. Miklavič, T. Pisanski and P. Šparl (EMS Press, 2023); pp. 511–534. Accessed on Oct 5, 2023.
O. Salazar Celis. Numerical Continued Fraction Interpolation. Ukrainian Mathematical Journal 76, 635–648 (2024). Accessed on Jan 28, 2025.